Contents
|
|
In this guide, we will be going deep into symmetric and asymmetric cryptography and the science behind cryptocurrencies cryptography.
Cryptocurrencies like Bitcoin and Ethereum use a peer-to-peer decentralized system to conduct transactions. Since the entire process is online, there are fears that the transactions maybe volatile and hackable. What we are going to see in this guide is how cryptocurrency uses cryptography to make their transactions extremely secure.
Digital Signatures
One of the most important cryptographical tools that are used in cryptocurrency is the concept of signatures. What is a signature in real life and what are its properties? Imagine a paper that you have signed with your signature, what should a good signature do?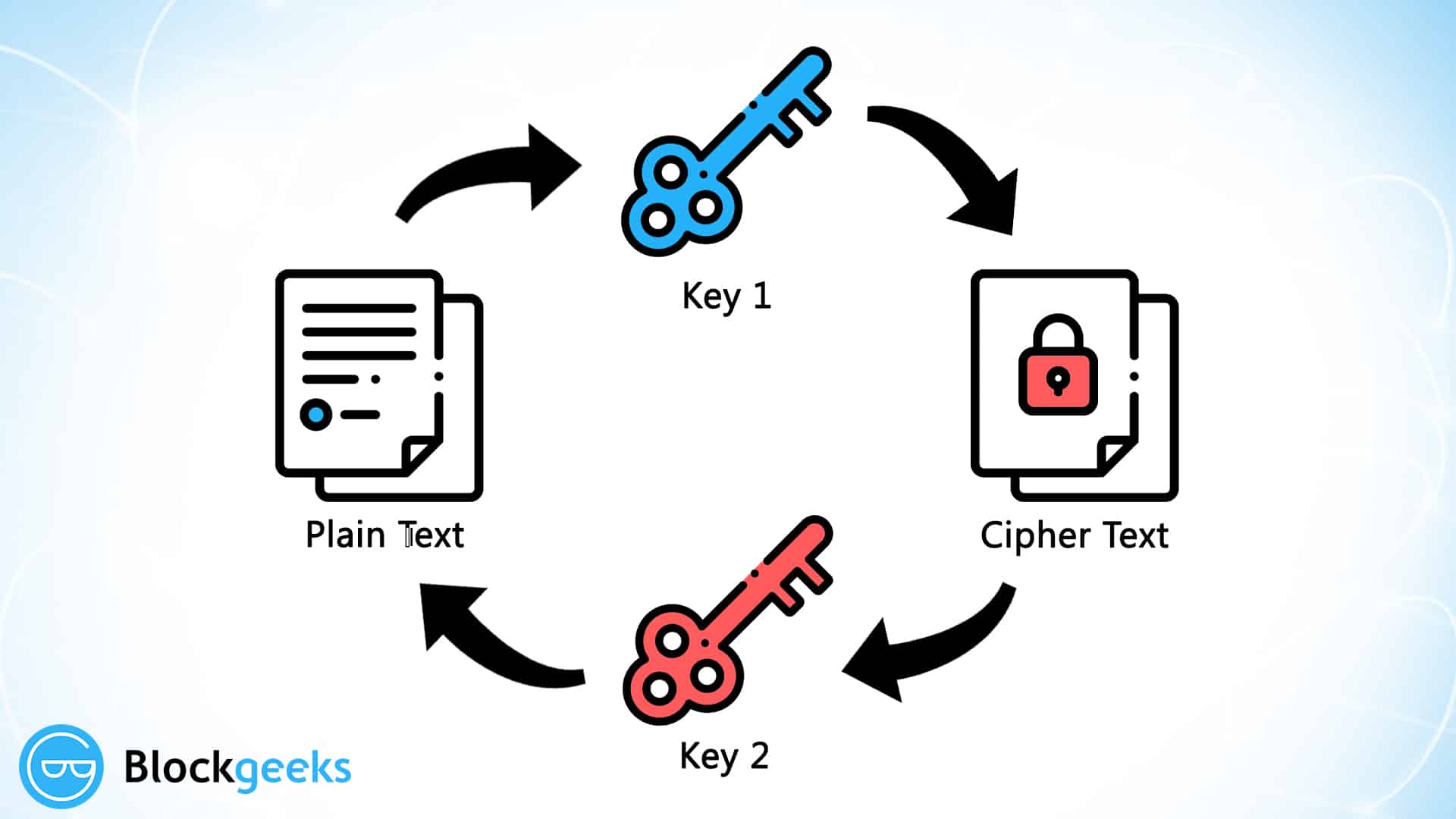
- It should provide verification. The signature should be able to verify that it is you who actually signed the paper.
- It should be non-forgeable. No one else should be able to forge and copy your signature.
- Non-repudiation. If you have signed something with your signature, then you should not be able to take it back or claim that someone else has done it instead of you.
In the real world, however, no matter how intricate the signature, there are always chances of forgery, and you cannot really verify signatures using simple visual aids, it is very inefficient and non-reliable.
Cryptography gives us a solution to this by means of “digital signatures” which is done via the use of “keys”. So, what are keys? And how are the used in the blockchain? Before we explore those, it is important to know more about basic cryptography.
Contents
What is Cryptocurrencies Cryptography?
Cryptography is a method of using advanced mathematical principles in storing and transmitting data in a particular form so that only those, for whom it is intended for, can read and process it. Cryptography has been used for thousands and thousands of years by people to relay messages without detection. In fact, the earliest use of cryptography was seen in the tomb taken from the Old Kingdom in Egypt circa 1900 BCE. Cryptography has existed in modern society through one way or another.
Encryption is one of the most critical tools used in cryptography. It is a means by which a message can be made unreadable for an unintended reader and can be read only by the sender and the recipient. In modern technology, there are three forms of encryption that are widely used: symmetric cryptography, symmetric cryptography, and hashing.
Symmetric Cryptography
Symmetric cryptography is the earliest known cryptographic method known to man. The concept is very simple and if we were to break it down to steps, this is what it will look like:
- You have a message M that you want to send over to your friend.
- You encrypt the message with a Key and get a cipher text C.
- Your friend gets your cipher text C.
- She then decrypts the cipher text using the same Key to retrieve message M.
If we were to show a visual representation of the process, this is what it will look like.
Image credit: SSL2BUY
The are two types of symmetric cryptography:
- Stream Ciphers.
- Block Ciphers.
What is stream ciphers?
Stream cipher basically means using a fixed key which replaces the message with a pseudorandom string of characters. It is basically the encryption of each letter one at a time.
We are going to discuss 3 kinds of stream ciphers in this guide to give you an idea of how stream ciphers work:
- One-time pad with alphabets.
- One-time pad with XOR gate.
- Linear feedback shift register.
One-time pad with alphabets
For doing this encryption we need to have a key which has the same number of characters as the message and it must be used one time only (hence the term “one-time pad”).
Suppose for this example we are going to send a message, “MEET ME OUTSIDE” to our friend Bob. But we don’t want anyone intercepting our message. This is why, Bob and us have decided to use a one-time pad which goes like this:
“B D U F G H W E I U F G W”
As you can see, the pad has the same number of characters as the message as well, i.e. 13.
Now, this is a very simple example of the one-time pad, we are using this because we feel it is the best example to use to understand this tactic.
Now, one more thing you need take note of, every alphabet will be replaced by its numeric equivalent in during the process.
The numerical mapping goes like this:
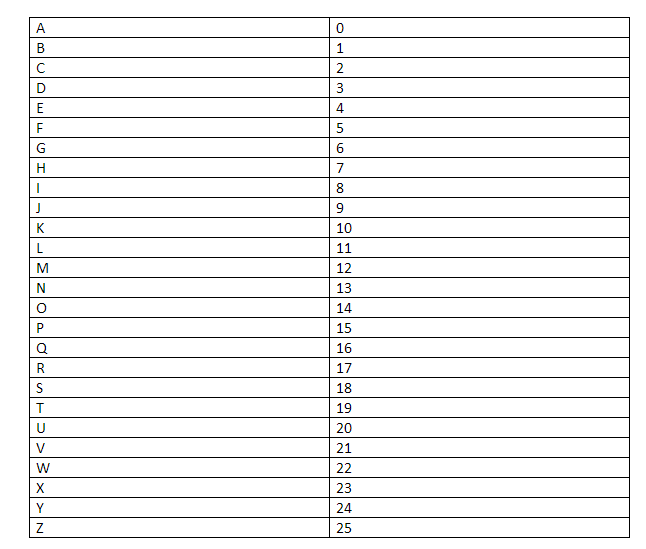
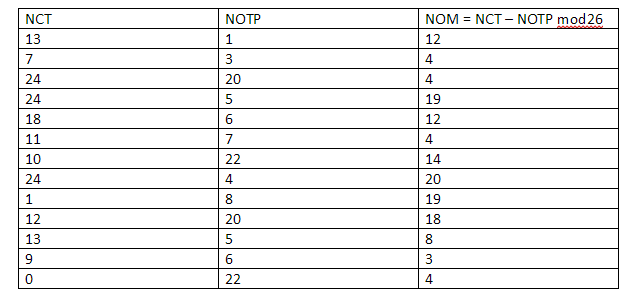
During the process, there will be 6 pieces of data that we need which are: Basically, the numerical equivalent of each alphabet. Ok, now that we have built the foundations, let’s move on to the actual process.
- Original Message (OM): The original message that we are passing through. In this case “MEET ME OUTSIDE”.
- Numerical Original Message (NOM): The numerical equivalent of the original message,
- OTP: The One-time Pad.
- Numerical OTP (NOTP): The numerical equivalent of the OTP.
- NCT: The numerical cipher text which is NOM+NOTP mod 26
- CT: The cipher text which is the alphabetical equivalent of the numbers in the NCT.
So, we need to send the message “MEET ME OUTSIDE” and we need to use the one-time pad to encrypt it.
The encryption process
So, let’s start off by putting in the message in the OM
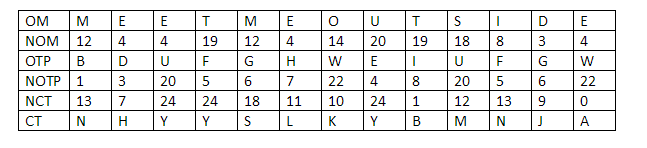
We put the message “MEET ME OUTSIDE” in the OM row.Ok, so what happened here?
Next, we used the numerical mapping table to get the numerical equivalent of each alphabet. So, let’s refer to the mapping table and see what we get:
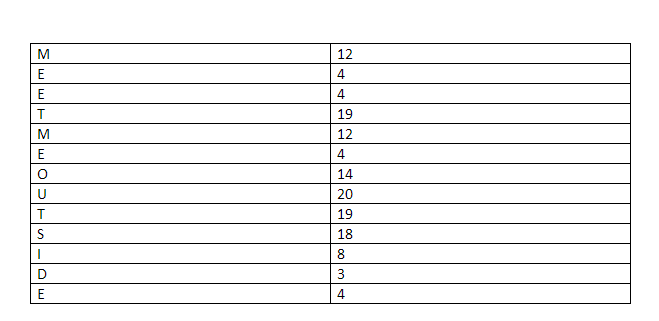
In the OTP row we put in the key that we were already given which is, in case you have forgotten, “B D U F G H W E I U F G W”.It’s just simple substitution, we will take these values and put it in NOM row.
Now, in the NOTP row we used the same number mapping table and found the equivalent numerical values of the key which are:
“1, 3, 20, 5, 6, 7, 22, 4, 8, 20, 5, 6, 22”.
In the new row, for the Numerical cipher text (NCT) we add the NOTP and NOM and mod the result by 26 to get our NCT.
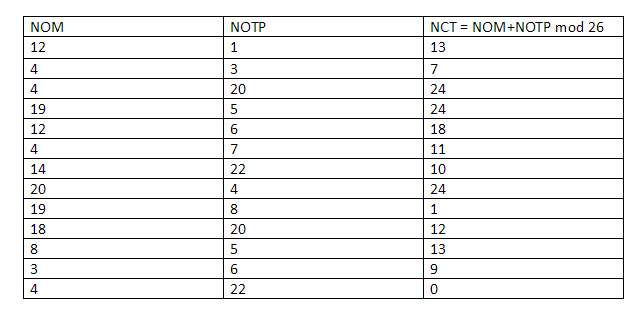
So, finally the message “MEET ME OUTSIDE” turns into a pseudo-random series of characters “N H Y Y S L K Y B M N J A”.That’s how you find the values for NCT and then you use the mapping table and find the corresponding alphabets which are: “N H Y Y S L K Y B M N J A”.
That is how the encryption process works.
The decryption process
Now we will see how we can decrypt the message using the exact same key.
Let’s see the data that Bob has with him:
- He has the encrypted message that he has gotten from me.
- He has the key that both of us share.
- He has the mapping table to find the numerical equivalents.
So, how will he decrypt the message using this data?
- He will map the numerical values of both the key and the encrypted message to get NCT and NOTP.
- He will then calculate the NOM (Numerical value of the original message) by doing this calculation: NOM = NCT – NOTP mod 26.
- He will use the mapping table to retrieve the corresponding alphabets.
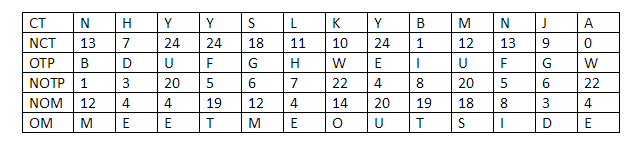
So, let’s see how the NOM calculation work?
Now, if we map the NOM to its alphabetical equivalent using the mapping table then we get:
“MEET ME OUTSIDE”
And just like that, the message is encrypted and decrypted using the same key.
One-time pad with XOR gate
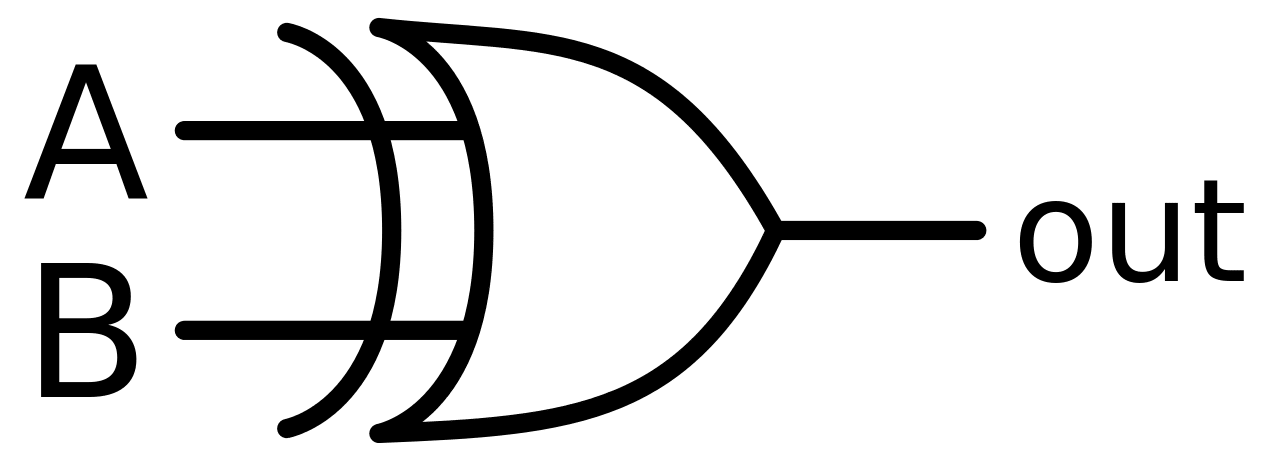
XOR or “Exclusive OR” is a logic gate. What is a logic gate? A logic gate usually takes in 2 inputs and gives out 1 output. The inputs and outputs are binary values, meaning they can be 1 or 0. A XOR logic gate takes in 2 binary inputs and gives out a high output ONLY when the inputs are different. Meaning, if A and B are inputted to a XOR gate then the out C will be 1 ONLY when A is not equal to B.
The XOR gate looks like this:
Image courtesy: Wikimedia
This what the XOR truth table look like:

The encryption process
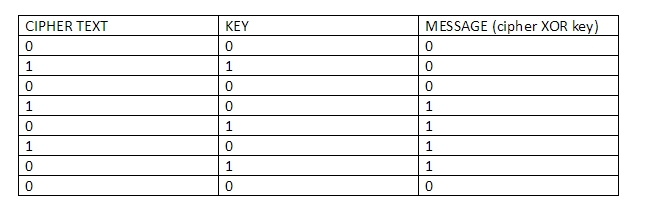
Suppose you have a plain text data which you want to send to your friend Alice. First, you’ll convert it to its binary form. Suppose the message that you have is this: 00011110
Now you have the key, the key that you share with your recipient and suppose you have passed the key through an algorithm which gives you the equivalent binary result: 01001010.
So now that you have the key, you are going to XOR each corresponding individual bits to get the resulting cipher text output.
Cipher Text = Plain Text XOR Key
So if you XOR both the data the key that you will get is:
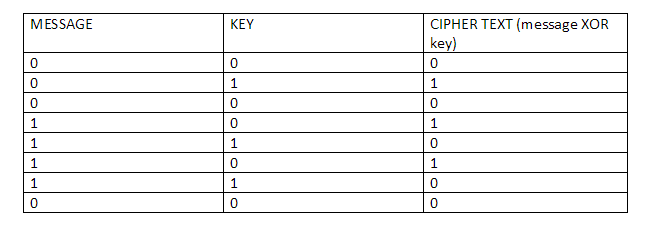
“01010100”
This is the cipher text that Alice will get from you.
The decryption process
So now, how will Alice decrypt your message and retrieve the original one?
This is the data that she has:
- The cipher text
- The key.
So what is she going to do? It is simple.
She will simply XOR the key and the cipher text and she will retrieve the original message! See for yourself:
And just like that, she will retrieve the original message.
Linear feedback shift register
What is a linear feedback shift register? It is a function whose future output completely depends on its earlier (or current) state. This will become clearer as you keep reading so don’t get scared off!
The idea of this style of a stream cipher is to predetermine a key with your recipient which will be a linear feedback shift register function which will be used by you to determine the code. Suppose you spoke to your friend Bob and determined that this is the formula that you both want to go with (credit to Daniel Rees from Youtube for this formula).
- E(i+3) = E(i+1) + 2E(i+2) mod 26.
And let’s also assume that prior to sending this message you and Bob determined that E(1) = 2 and E(2) = 4.
Now you can see that in this equation, all future outputs are dependent upon the previous outputs.
So, suppose the message that you want to send to Bob is “MEET ME”. Since there are 6 characters, we need to determine 6 values of E() to act as key. We already have predetermined the values of E(1) and E(2). Now we need to calculate E(3) to E(6).
- E(3) = E(1) + 2E(2) mod 26 = 10.
- E(4) = E(2) + 2E(3) mod 26 = 24.
- E(5) = E(3) + 2E (4) mod 26 = 6.
- E(6) = E(4) + 2E(5) mod 26 = 10.
So, now that we have the keys, let’s start the decryption.
The encryption process
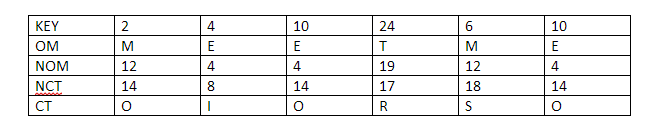
So now that we have the key and message, let’s create the table:
To get the numerical cipher text, you add the key and the corresponding numerical value of the alphabet that you map from this table that we have already seen before:
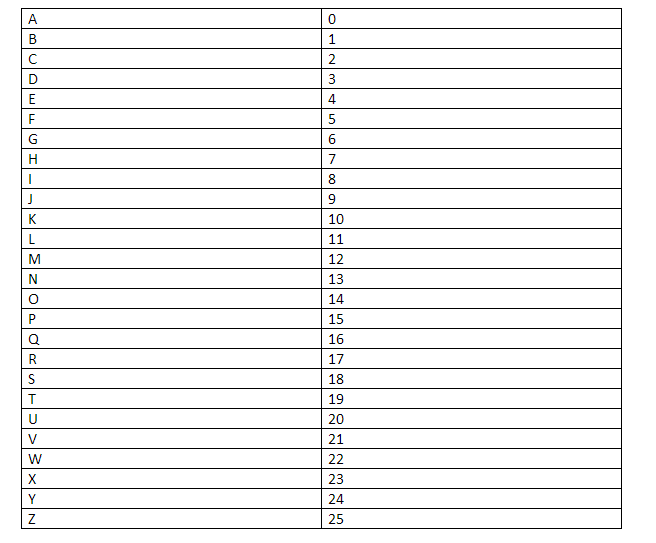
Now, to get the numerical value of the cipher texts, add the key and the numerical value of the original message and mod with 26.
So you get:

Now use the mapping table again to find the corresponding alphabets and you get “OIORSO”. That’s the encrypted message.
The decryption of this message is really hard especially if you don’t have the key. An expert might spot a pattern though. You will need computers to beak this code.
Examples of Stream Ciphers used in the real world.
The Rivest Cipher 4 of the RC4
- Used in WEP aka wired equivalent protocol for wireless network security.
- Also an option in TLS/HTTPS for encrypting web traffic.
- Since it has been cracked so many times it is not recommended for use anymore.
The A5/1
- Use for encrypting GSM (Global System for Mobile communication) phone data and communication.
- Edward Snowden in his leaks revealed that the NSA routinely keeps breaking GSM for surveillance purposes so it is not a secured mode of encryption anymore.
So, that is pretty much it about stream ciphers, time to move on to block ciphers.
What is block ciphers?
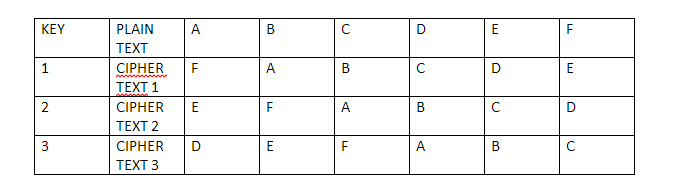
Block ciphers are a form of symmetric cryptography which uses a key of a fixed length to encrypt a block of fix length. Let’s start by checking out a very common substitution cipher that you must have seen before:
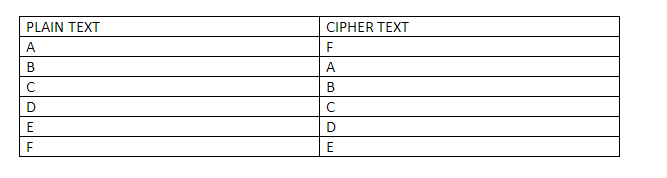
So, if someone were to tell you that they got a message which says “EFBD” and wants you to decrypt it and get the original message instead, how will you do it?
You will simply see the table, see which alphabets correspond to which and then simply substitute right? So “EFBD” is the cipher for “FACE”.
Now let’s check out the plain text and the ciphertext and compare them:
- Plain: A B C D E F
- Cipher: F A B C D E
So, as you can see, the cipher text is basically the plain text shifted the right by one. So, in this particular case:
- EFBD = FACE shifted by 1
That, in essence, is what a block cipher is. Given an input plain text and a key it can generate a unique cipher text. One more thing that is extremely important and should be noted. Given the key, anyone can decipher the cipher text from the plain text and vice versa. The examples that we are giving here are all extremely simplistic, the block cipher happens with HUGE chunks of data.
If we are looking for a visual representation of a block cipher the this is what it will look like:
Another interesting property of the block cipher is that if the key changes then that changes the output cipher text pretty drastically. Let’s do a test with the data we have right now.
Now, we have 3 keys for the 3 different cipher texts.
- In cipher text 1 we are shifting to the right once.
- In cipher text 2 we are shifting to the right twice.
- In cipher text 3 we are shifting to the right thrice.
So, let’s see what happens when we parse the input “FACE” through all these different ciphers.
- When key =1, FACE becomes EFBD
- When key = 2, FACE becomes DEAC
- When key = 3, FACE becomes CDFB
As you can see, the output cipher text changes everytime you change the key. In the example we have very little data, imagine doing this with HUGE amounts of data, the output will change drastically every single time.
There are two rules for a block cipher to be considered valid:
- You must be able to derive the plain text from the cipher text and vice versa given a key.
- The function must be efficiently computable.
There is one more important thing that you need to take note of when it comes to block ciphers. The block sizes are fixed so the input plain text needs to be of the same size as the block size. If the input is bigger than the block then it needs to break down to get the correct size, if the input is smaller, then it needs to be padded with some junk data to fit the block size.
Examples of block ciphers
Data Encryption Standard (DES)
- Block sizes of 64 bits.
- Key size of 56 bits.
- Was the government standard till 2001.
Advanced Encryption Standard (AES)
- 128 bit blocksize.
- 128, 192 or 256 bit key size.
- Considered very secure and widely used nowadays
The advantage of symmetric cryptography
Even though symmetric cryptography has some major problems (which we will discuss in a bit) the biggest advantage of symmetric cryptography is that it requires very little overhead. You just need to share one single key with your recipient to go forward with this method.
Even now, a lot of software use this method in conjunction with asymmetric cryptography to provide fast and efficient encryption/decryption services.
The problems with symmetric cryptography
Even though the overhead is significantly lesser, there are a lot of problems with symmetric cryptography.
Problem #1: The shared key
The fact that the encryption and decryption is done with one single key is a huge problem. First and foremost, the sharing of the key needs to be done in a very secured manner, if anyone gets hold the of key then all your data will be compromised.
Problem #2: It is not scalable
Another huge problem with symmetric cryptography is that it is not scalable at all. Suppose Alice runs an information center and sends data via symmetric key cryptography. It’s ok if she is only dealing with 3-4 clients. But the most clients she gets, the more unique public keys she will have to handle and take care of. Eventually, it will become too much to handle.
Because of these vulnerabilities of symmetric key cryptography, a solution was needed, and in the 1970’s it finally came.
James Ellis’s breakthrough
In 1970, British mathematician and engineer James Ellis thought of an idea which was based on a simple concept. What if encryption and decryption were inverse operations based on 2 different keys? In traditional cryptography i.e. symmetrical cryptography, the message had to be sent along with the key to the intended person for them to decrypt the message, but this presented the very real idea of an attacker getting their hands on the key.
Ellis envisaged that the receiver of the message couldn’t be a passive party, and they had to have a “padlock” and a “key” for themselves. The padlock could be sent to anyone in the world but the key had to be kept private. So, anyone can send a message to the receiver by locking it with their padlock and since only the receiver has the key, only they can open it.
Now, this was the theory, there needed to be a practical form of this theory, and that came because of two brilliant principles:
- The trapdoor function.
- The Diffie–Hellman key exchange.
What is the trapdoor function?
A trapdoor function aka a one-way function is a function where it is easy to go from one state aka the domain to the other state aka the range but it is hard to go back from the range to the domain unless you have knowledge of a key which is called the trapdoor function.
Diagrammatically it is represented like this:
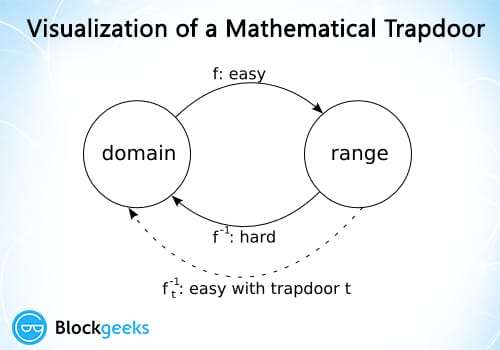
Image credit: Cornell.edu
The trapdoor functions are based on the idea of keys. Wherein the public key (K) is used to go from the domain to range. In order to come back to the domain from the range we have to use a trapdoor function which is also known as the private key (k). It is also implied that the private key and public key are mathematically related to each other and also they have to related to each other via another trapdoor function f() such that K= f(k) so that the private key is infeasible to be determined by the public key.
A simple example of this is a multiplication of large numbers. Suppose you have two numbers 171 and 118 then it is simple to determine that 171 * 118 = 20178. However, if you just know 20178 then it is hard for you to determine what the initial numbers were unless you have a key with you, in this case the knowledge of just one of the two numbers, to determine the second one.
What is the Diffie-Hellman key exchange?
Suppose, there are two people Alice and Bob and they want to attack a bank. However, they are on either sides of the bank and they can only communicate with each other via a shared line which is being tapped by the bank.
Something like this.
Keep in mind, everything that Alice and Bob say to each other will be eavesdropped upon by the bank. So, how can they both decide on a date to attack the bank without the bank getting to know about it and without Alice and Bob explicitly exchanging that information?
This conundrum can be answered by the Diffie-Hellman key exchange; it is a concept by which two parties can get hold of secret information without sharing it.
To understand how the Diffie-Hellman works, we need to use one of the most famous applications of this theory, the secret colour exchange.
For this there are 3 things that you need to keep in mind:
- Alice and Bob both publicly agree that yellow is going to be the common paint that they are both going to use.
- Alice then secretly keeps to herself that she is also going to use orange along with yellow.
- Bob secretly decides that he is going to use aqua along with yellow.
Stage One
Since it was publicly declared that yellow is going to be the colour of choice:
- Bank: Has Yellow
- Alice: Has Yellow
- Bob: Has Yellow
Stage Two
Now Alice mixes in her private colour aka orange with yellow and gets a composite colour which we will call CA.
At the same time, Bob mixes his private colour aqua with yellow and creates composite colour CB.
So, at the end of stage two this is what things look like:
- Bank: Yellow
- Alice: CA
- Bob: CB
Stage Three
Now, Alice and Bob will send each other their respective colours, which will promptly get tapped by the bank. However, the bank now faces a problem.
Colour combinations are a trapdoor function.
While it is easy for someone to combine two colours and generate a third colour, it is infeasible for them to determine the first two colours from the given third colour. So, the bank will get hold of CA and CB but will have no idea which are the colours that has gone into its creation.
So, this is what things are looking like right now:
- Bank: Yellow, CA, CB.
- Alice: CB
- Bob: CA.
Stage Four
Now, Alice and Bob are once again going to mix their secret colours into the mix that they have received from the other person, so now both of them are going to have a mix of yellow, orange and aqua which is brown. The bank, however, will only have CA and CB because they have no idea what the secret colours are.
So, this is what things look like now:
- Bank: Yellow, CA and CB.
- Alice: Brown.
- Bob: Brown.
And this is where the trick lies, by not revealing their secret colours, both Bob and Alice have, in their possession, the colour brown, even though they never explicitly exchanged brown with each other.
This is what the diagram of this entire exchange looks like:
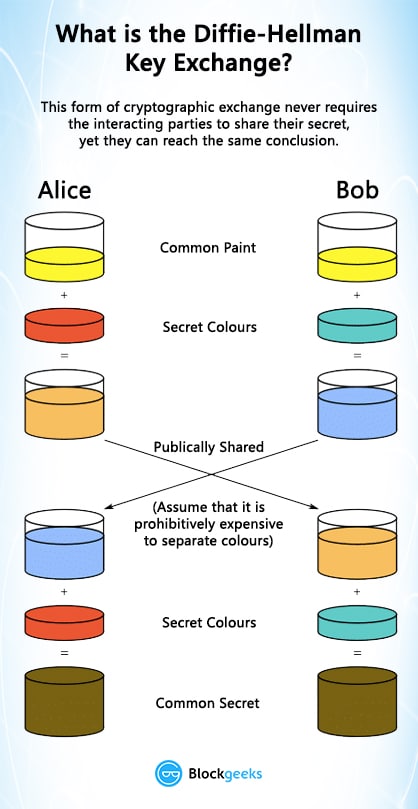
Image Courtesy: Wikipedia
This is the representation of the Diffie-Hellman exchange, but a mathematical means was needed to make sure that there could be practical applications of this as well. For this reason, the modulus function was used.
The mathematical form of the Diffie-Hellman exchange
Suppose there is a generator g for a finite field of size n. And in that field, we choose two random values a and b. It will be hard for an attacker to determine g^ab given only g, g^a and g^b. This is the condition which activates the trapdoor function. Given this condition, two parties can exchange messages and reach the same conclusion without explicitly communicating it with each other.
So, mathematically this is what happens.
Alice chooses a random value “a” from the field n and determines a message M1 such that:
- M1 = g^a mod n.
Similarly, Bob chooses a random value “b” from the field n and creates message M2 such that:
- M2 = g^b mod n.
Both Alice and Bob can now relay the message to each other.
Alice now determines special message K by doing the following:
- K = M2^a mod n= g^ab mod n.
Bob now determines the same message K by:
- K = M1 ^ a mod n = g^ab mod n.
So, both Alice and Bob reached the same conclusion without explicitly sharing this information.
This Diffie-Hellman key exchange was invaluable in the formation of asymmetric cryptography:
What is asymmetric cryptography?
Asymmetric cryptography utilizes two keys, a public key and a private to encrypt and decrypt a particular data. The use of one key cancels out the use of the other.
The diagrammatic representation of it looks like this:
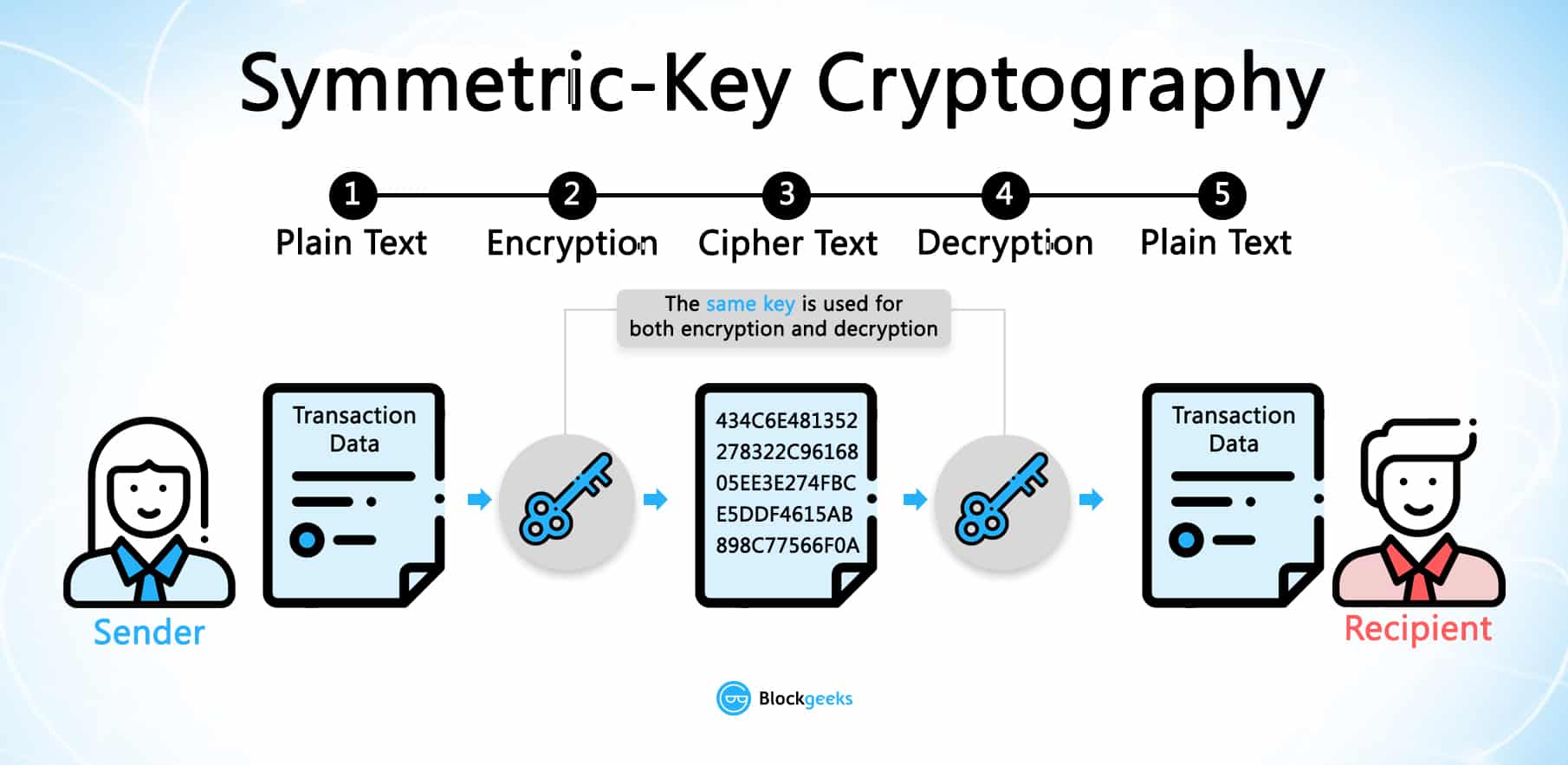
Image courtesy: SSL2BUY
There are two real world use of asymmetric cryptography that we will look into in this guide and both are important for their own reasons:
- The Rivest-Shamir-Adleman algorithm aka the RSA.
- The Elliptical Curve Cryptography.
What is the RSA algorithm?
The RSA algorithm is the most widely used and popular asymmetric cryptographic algorithm in history. It is named after MIT professors Rivest, Shamir and Adleman who discovered this algorithm. Now, how does it work? The idea is derived from the breakthroughs that Diffie-Hellman had.
So, these are the variables that we will work with:
Suppose you have the secret message “m”. “m” raised to the power of a random number e and then the modulus of that with a random number N will give you the cipher text c.
Basically. m^e mod N= c
Take note, it is EASY to perform this function to get the output c BUT given only c, e and N it is difficult to get the message “m”. It will require a lot of trial and error. This is the one-way trapdoor function that we will apply to find “m”.
But now, the idea of the trapdoor function is to have a key which will make the reverse process (the decryption) simple for the recipient. So, for that we will need to find a random variable “d” which will make this process possible:
- c^d mod N = m.
Now keep in mind, c = m^e mod N, so on substituting.
- m ^ e ^ d mod N = m.
OR
- m ^ ed mod N = m
So, in the above equations:
- Public key = e and N.
- Private key = d.
Now, before we even begin to see the method behind the madness, let’s do a simple calculation to see how the entire process works. (Shout out to Anthony Vance’s youtube channel for this example).
Suppose the message that you have to send is 42. In other words, m=42.
Along with that:
- e = 17.
- N = 3233.
- d = 2753
The encryption process
c = m^e mod N.
Using simple substitution:
c = 42^17 mod 3233 = 2557.
So the cipher text is 2557.
The decryption process
Let’s do c^d mod N.
2557^2753 mod 3233
This gives us the value of m that is 42.
Genius isn’t it?
Now, remember when we talked about trapdoor functions we came to the conclusion that private and public key needs to be mathematical derivatives of each other in a way that:
F(private key) = public key, where F() is another trapdoor function.
It should be difficult for anyone to determine the private key from the public key. In fact, it should be so difficult that it will take the world’s most powerful computer decades upon decades to derive one from the other.
To answer this conundrum, we go back centuries and meet our next genius, Euclid.
Euclid and prime factorization
Euclid found out centuries ago that any number > 1 can be written as a product of prime numbers.
- Eg. 15 can be written as 5*3.
- 255 can be written as 5*17*3.
Let’s go back to our two equations:
C= m^e mod N.
Here, N is the key in the trapdoor function. While N maybe publicly known it should be hard to determine prime factors that make up the number N. If you know the prime factors, then it is child’s play to discover the product N.
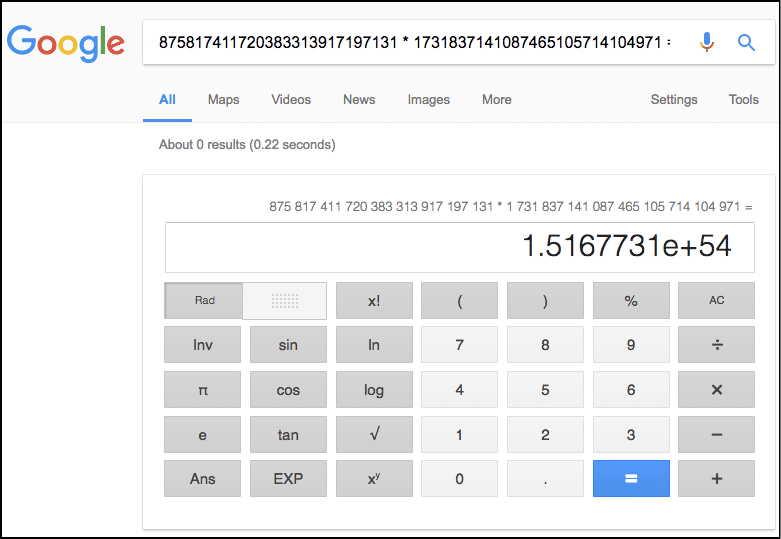
Eg. You can use your web browser to multiply two huge numbers and find the product in less than a second:
It took less than a second, 0.22 seconds, to do the calculation. And the bigger the number gets, it will take a little more time, but still, the calculations will be done super fast.
However, if you input a huge number and ask your computer to find its prime factors then it may take days, months and even years to find the prime factors.
This is the trapdoor function that cryptographers used to determine the value of N. This is basically, the heart of the trick.
This is what you have to do to use RSA algorithm:
- First, generate a big random prime number P1.
- Generate a second big random prime number P2.
- Find N by calculating P1 and P2.
- Hide the values of P1 and P2 and make N public.
- N should be a huge number and it will take the most sophisticated machines in the world decades to find the values of P1 and P2.
- So to summarise, N is the trapdoor and its prime factors P1 and P2 are the keys to the trapdoor.
Ok, so now we have determined how N is calculated and the trapdoor that works in it. But we still haven’t determined the value of “e” and “d” and we still haven’t seen how the private key is derived from the public key. In order to generate all these remaining values, we need to find a function that depends on knowing the factorization of N. And for that we need to go and visit our next genius, Leonhard Euler.
Euler and breakability
In 1760, Swiss mathematician Leonhard Euler did some path breaking studies. He studied the nature of numbers and more specifically the breakability of the numbers which he called the phi function.
Basically given phi(N) where N is a random integer, the value of N will be the number of numbers between 1 and N which do not share any common factors with N.
So, if N is 8 then:
The numbers between 1-8 are: 1,2,3,4,5,6,7 and 8.
Among these numbers, only 1,3,5 and 7 don’t share any factors with 8 except 1.
Meaning, phi(8) = 4.
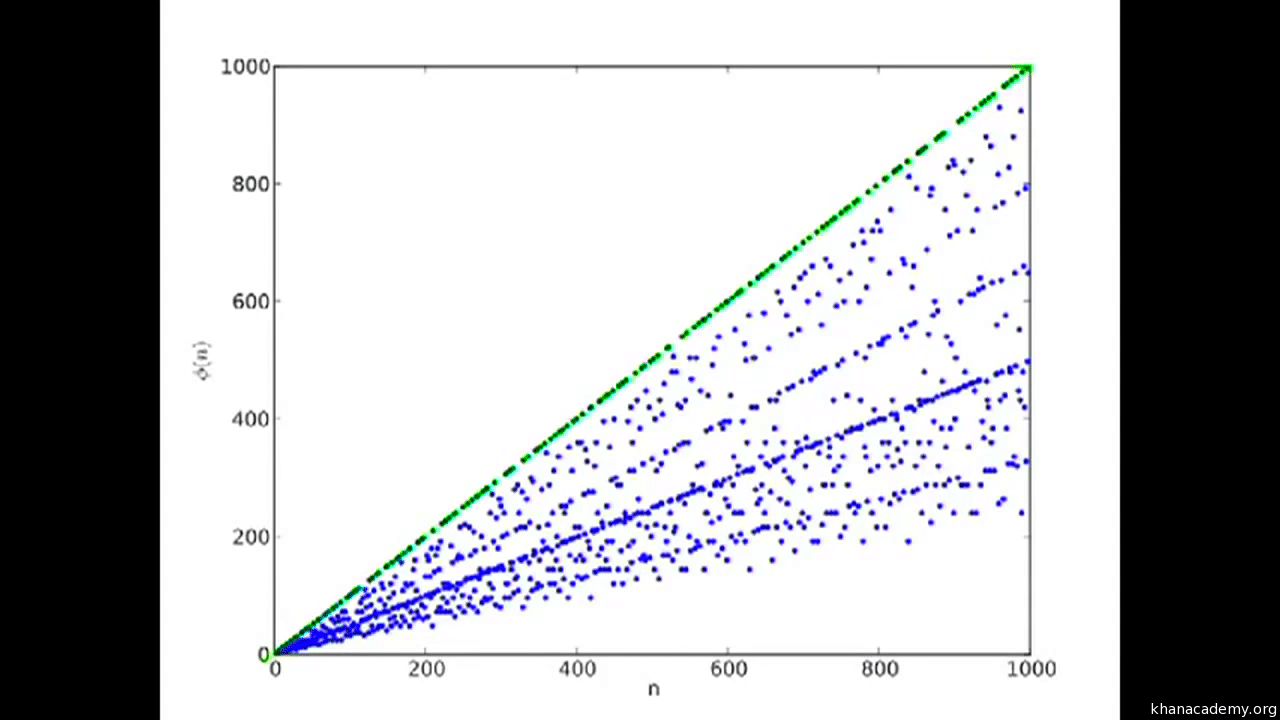
Now, calculating the phi function is difficult except for one case. To know this, check out the following graph. The graph tracks the distribution of phi values over integers upto 1000.
Image courtesy: Khan Academy
See that straight green line at the top which is conveniently arranged? That is the phi of prime numbers. Since the definition of a prime number is that it is unfactorizable apart from by itself, for any prime number p the phi(p) = p-1.
Let’s see this in practice. Suppose you have a prime number 7.
The numbers between 1 and 7 are: 1,2,3,4,5,6,7.
The only number that shares a factor with 7 in this series is…7!
So the phi(7) = 6.
Similarly, if you were to find the phi of a large prime number say 541 then:
Phi(541) = 541-1 = 540.
It becomes very simple to calculate the phi for a prime number. And this gains, even more, significance when you consider the multiplicative nature of phi functions. What is the multiplicative nature of phi functions?
For any two numbers A and B:
Phi(A*B) = phi(A) * phi(B).
Now, let’s go back to algorithms. Alice has determined two large prime numbers P1 and P2 and has determined a number N by doing P1 * P2.
So, using the multiplicative property of phi functions:
Phi(N) = phi(P1) * phi(P2).
OR
Phi(N) = (P1-1)*(P2-1).
And just like that, we have discovered the trapdoor function for phi. If we know the prime factors of N then it is easy to calculate the phi(N).
For eg. the number 77 has prime factors 7 and 11.
So phi(77) = (7-1)*(11-1) = 60.
It becomes very easy when you know the prime factors of N.
Now, one final bit of mathematical wizardry was required. We have the phi function and we have the modular exponentiation functions that we have determined before, we need to bring these two together in one neat equation.
And for this, we turn to Euler for help once again.
The Euler’s theorem
Euler’s theorem states that:
For any two numbers m and n that don’t share a factor:
m ^ phi(n) ≡ 1 mod n
Meaning, for any two numbers m and n, as long as they don’t share a factor, m raised to the phi(n) divided by n will always leave a remainder of 1. Let’s see this in an example.
Suppose, m= 8 and n = 5.
Phi(5) = 4
So, 8 ^ 4 = 4096.
Replacing this in the Euler’s theorem equation:
4096 ≡ 1 mod 5 holds true because 4096 on being divided by 5 leaves a remainder of 1.
Now, the equation: m ^ phi(n) ≡ 1 mod n needs to be modified a little bit before we get our final solution.
Modification #1
1^k = 1 for all k.
So, keeping this in mind, if in m ^ phi(n) ≡ 1 mod n we multiply the exponent phi(n) with any number k, the final solution will be 1^k which is still 1.
Now, this modifies the equation like this:
m ^ k*phi(n) ≡ 1 mod n
Modification #2
For all m, m*1 = m.
So, in our modified equation, if we multiply both sides by m we get:
m*m ^ k*phi(n) ≡ m*1 mod n
Which becomes:
m ^ k*phi(n)+1 ≡ m mod n
Now, this is the final form of our equation.
Before we proceed, let’s bring back the old equations to refresh our memory:
- c = m^e mod N.
- m = c^d mod N
- m ^ e*d mod N = m
Now, checkout the last equation doesn’t that look similar to our new modified equation:
m ^ k*phi(n)+1 ≡ m mod n
And this is the breakthrough.
On comparing the two equations, we get:
e*d = k*phi(n) + 1
We FINALLY have an equation where the value of e and d depends on phi(n).
Now, since we already know the value of e, it is easy to calculate d, the private key, ONLY if the factorization of N is known (which is a secret that Alice has kept to herself).
So, d= (k*phi(n) + 1)/e.
This is the trapdoor that will undo the encryption done by her private keys e and n.
Example to see how this all works
Suppose Bob and Alice are exchanging messages.
Bob wants to send a message M to Alice where M=89.
Now, Alice needs to generate her keys.
She uses to prime numbers p1 and p2 where:
P1 = 53.
P2 = 59.
N = P1 * P2 = 53 * 59 = 3127.
Phi (N) = Phi(P1) * Phi (P2) = (P1 – 1) * (P2 – 1) = 52 * 58 = 3016
Now, she needs to generate a value e which will have no factors with the value of phi(N).
So, she decides e = 3.
Now, she will generate her private key d:
d = (k*phi(N) + 1)/e
Taking k = 2 we get:
d = (2* 3016 + 1) / 3 = 2011.
Now, she will lock up all the values except N and e which are her public key and make the knowledge of these two global.
Bob encrypts the message
Now, Bob needs to send message M, which is 89, and he needs to calculate the cipher text c such that:
c = M^e mod N.
Now, we know that: M = 89, e = 3 and N = 3127.
So: c = 89^3 mod 3127 = 1394.
He then sends it over to Alice.
Alice decrypts the message
Alice gets the cipher text and all that she has to do is to decrypt it using her private key d which we know to be 2011.
So, Alice does this calculation: c^d mod N
1394^2011 mod 3127 which is 89 aka the original message M.
And this, is the RSA algorithm, the most widely used cryptographic algorithm
What is elliptical curve cryptography?
Elliptical curve cryptography is what is used by bitcoin, ethereum etc. for their encryption purposes. So what is an elliptical curve? An elliptical curve is any curve that satisfies the following equation:
Y^2 = x^3 + ax + b
Where (x,y) is a point on the curve and a and b are constants.
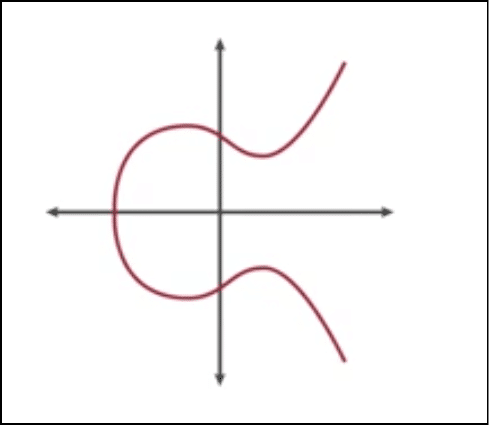
There are infinite curves that you can make. The following is how one of these curves, in general, look like:
Image credit: CSBreakdown youtube channel
What are the properties of an elliptic curve?
- The curve is symmetric across the x axis.
- Any line that goes through 2 points on the curve will intersect the curve on a third point.
- Any tangent on the curve will intersect the curve on one more point.
Performing maths on the curve.
Addition property of the curve
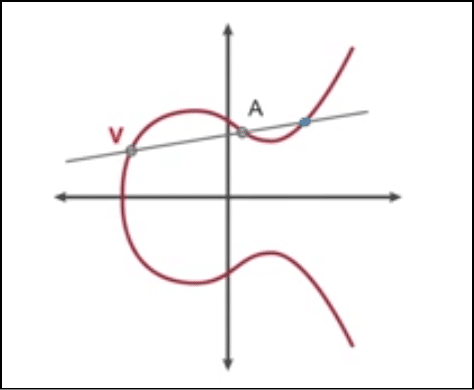
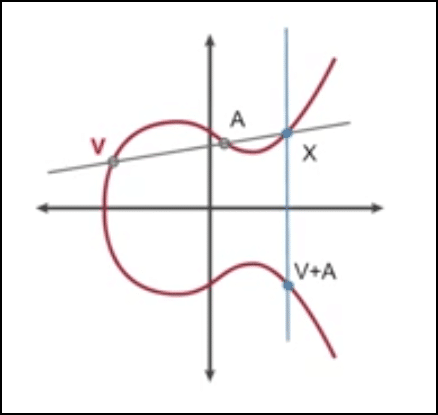
Suppose there are two points on the curve V and A. Let’s trace those on the curve and put a line through them. This will intersect the curve on a third point.
Image credit: CSBreakdown youtube channel
We will call this third point X, and we will reflect it on the curve like this:
Image credit: CSBreakdown youtube channel
The reflection of X is a point which will incidentally be (V+A). This is the additive property of the elliptical curve.
Interesting note. If we add two reflections with each other aka if we were to add X and V+A in the graph above, we will get infinity. The reason for that is that the line through X and (V+A) will intersect the curve at infinity.
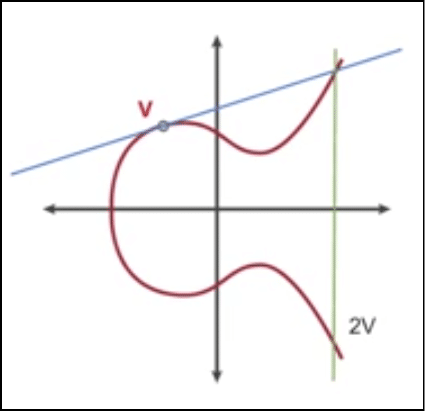
Multiplication property of the curve
Now, what if we want to add a number to itself? Like suppose we have a point V, what do we do to find 2V? We will run a tangent through V and intersect it at a point in the graph and then find the reflection of the point on the curve. That reflection will be 2V.
Image credit: CSBreakdown youtube channel
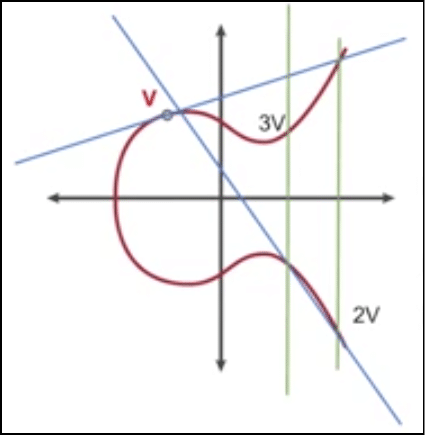
This is also the multiplicative property of the graph because we are finding points which are basically the multiplication of an integer with the point itself. Now suppose we want to find 3V. We will join V and 2V and then reflect the point of intersection, like this:
Image credit: CSBreakdown youtube channel
You see how the points cycle across the graph? This is what gives it its security.
Mathematical properties of an elliptical curve
Property #1: The points on the curve form an Abelian group
The properties of the Abelian group are as follows:
- They have identity.
- The have inverses aka reflections.
- The points are associative meaning for three points A, B and C on the curve: (A+B) + C = A + (B+C).
- The points are closed on the curve.
- The points are commutative meaning for two points A and B. A+B = B+A.
Property #2: Multiplication on the curve is fast
All multiplication done on the curve can be done very fast. Now suppose we have a point P and we want to find 100P. Instead of adding the number to itself 100 times we can do the following:
- Add the point P to itself to get 2P.
- Add 2P and P to get 3P.
- Add 3P to itself to get 6P.
- Add 6P to itself to get 12P.
- Add 12P to itself to get 24P.
- Add 24P and P to get 25P.
- Add 25P to itself to get 50P.
- Add 50P to itself to get 100P.
So, instead of going through 99 steps you cut short the entire thing to just 8 steps.
Property #3: Division on the curve is slow
Whilst multiplication is fast, the division is very slow. Suppose we have Q = nP and we want to find the value of n by dividing Q by P. We can’t really do that. We will have to manually go through the numbers one by one to find a value which satisfies the equation. This makes it very slow. This is called the discrete logarithmic problem and this is what gives the curves its trapdoor function i.e. it is easy to multiply n and P to get Q but given Q and P it is infeasible to get n.
The elliptical curve Diffie-Hellman key exchange
So, till now we have seen the various properties of the curve and we have also seen that the curve has a trapdoor function. Now how do we determine whether it is usable for cryptography or not? Let’s test it out with the Diffie-Hellman key exchange. Suppose we have Alice and Bob and they want to both come up with a common secret without anyone knowing what it is and without explicitly exchanging its information with one another. How will they do that via elliptical curves?
- Firstly, they will publicly agree on a curve to use and a point P on the curve. This will be public knowledge and available to everyone.
- In secret, however, Alice will choose a secret point “a” and Bob will choose a secret point “b”.
- Alice will compute “aP” and send it over to Bob. Anyone can intercept this message, however, even with the knowledge of P they will never be able to determine the value of “a” because, as we have already determined, there is a trapdoor function which will make division infeasible.
- Similarly, Bob will come up with the value “bP” and send it over to Alice.
- Alice will then multiply her secret key to the message that she gets from Bob to get a(bP). Bob will do the same and come up with b(aP). Since all the points on the curve are Abelian: a(bP) = b(aP). And just like that, they have come upon a secret shared information.
So as we can see. The curve satisfies the Diffie-Hellman key exchange.
So how does signature verification work on the elliptical curves?
(Note: This is what specifically happens in bitcoin)
Before we see how the process works let’s checkout certain variables and their meaning that we will be using the following equations.
- Private key = d.
- Message = z.
- Public key = Q.
G will be a constant point on the graph which will be provided by bitcoin.
- “k” is a random number which will be generated automatically for every unique signature.
- “n” is another constant that will be provided by bitcoin.
Ok, so now let’s see how the maths behind the verification work.
Signing a message
Public key Q = dG. (it is impossible to get the private key from Q and G because division in infeasible).
Now we will multiply the G with the random number “k” and plot that point on the graph. The co-ordinates of that point are (x,y). i.e. (x,y) = kG
Next, we determine two values r and s such that:
r = x mod n.
s = (z + rd) k^-1 mod n
The reason why we generate r and s is because these are the co-ordinates of our signature.
So, we send the point (r,s) for verification.
Verifying a message
The verifiers will conduct a simple equation:
z*s^-1*G + r*s^-1*Q
The value of this equation will give us the point (x,y).
Now, the verifiers can simply compare the x co-ordinates. They don’t have the x co-ordinate given directly to them from the sender BUT they have the values of r and n.
And as we already know that r = x mod n, and then they can simply solve for x.
If the values of x match out, then this means that the signature is verified!
Bonus: A deeper look into the maths
Let’s check out the equation that the verifiers will have to do once again:
- Step 1: z*s^-1*G + r*s^-1*Q
We know that Q = d*G, let’s simply substitute the value.
- Step 2: z*s^-1*g + r*s^-1*d*G
We can take (z + r*d) common
- Step 3: (z + r*d)*s^-1*G
Now remember, we have already established that s = (z+r*d)*k^-1 mod n ,let’s substitute the values here:
- Step 4: (z+r*d)*(z+r*d)^-1*k*G
The (z+r*d)*(z+r*d)^-1 cancel each other out and we are left with:
- Step 5: k*G which is the co-ordinate (x,y) that the sender originally sent.
What could go wrong in Elliptical curves?
While it goes without saying that elliptical curves are the best mode of cryptography out there, the fact remains that it still has few vulnerabilities:
- What if a wrong curve was chosen? If the curve has a loop in it then there is a possibility that 1001P = P for any point P on the curve.
- A weak curve maybe is chosen which can be broken into.
It has its weaknesses but they are pretty manageable weaknesses.
RSA vs EEC. Why did bitcoin and ethereum go with elliptical curves?
The reason why EEC was chosen over RSA is because it offers the same level of security as RSA by consuming far less bits. Eg. for a 256-bit key in EEC to offer the same level of security RSA will have to provide a 3072-bit key. Similarly, for a 384-bit key in EEC the RSA will have to provide a 7680- bit key to provide the same level of security! As can be seen, EEC is far more efficient than RSA.
Fun Fact: The NSA has declared that a 384-bit key in EEC is strong and secure enough to encrypt top level secret documents.
How do the keys work in blockchain?
As mentioned above, bitcoin and ethereum use elliptical curve cryptography. So, what happens when someone sends you money on the blockchain? They send you the money to your public address which is basically the hash of your public key and some additional information. As we have seen above, the public key is derived mathematically from your private key.
Public and private keys are both large integer values and they are represented, for brevity’s sake, via the Wallet Import Format (WIF) which consists of letters and numbers. A sample private key and public address looks like this in WIF:
Obviously, you shouldn’t share your private key with the world like we just did! The private key is used to sign off on the transaction that the user wants to do. So, if someone has access to your private key, they can sign off on transactions using your private key and, in essence, steal from you. Also, as you can see, the private key is longer than the public address.
So, how is a public key derived from the private key in the blockchain? Let’s take the example of bitcoin for this specific example.
Suppose, Alice wants to generate her keys so that she can conduct transactions on the blockchain. This is what she will do:
- First, she will generate her 256-bit private key. She can either do so manually OR she will use an auto-generator. This is an example of a private address generator that you can find in a wallet-generator.net:
- Next, she will have to generate the public address which the algorithm inside that wallet will do automatically by following these steps.
- First, her private key will be parsed through the SHA 256 hashing algorithm to get a hash.
- Then hash will be parsed through the RIPE MD 160 function and a new hash will be generated and a copy of it will be kept aside, let’s call this PART A.
- Then the hash will be hashed through SHA 256 to generate another hash.
- Then the new hash will be hashed through SHA 256 again to generate another hash. The first 7 bits of this hash will be saved, let’s call it PART B.
- PART A and PART B will be added up and the result is the public address.
It is infeasible for this process to be reversed in a way that the public address can be used to generate the private key. It will take the world’s most powerful computer 40000000000000000000000000000000 years to complete this calculation! Safe to say your address and key are secure.
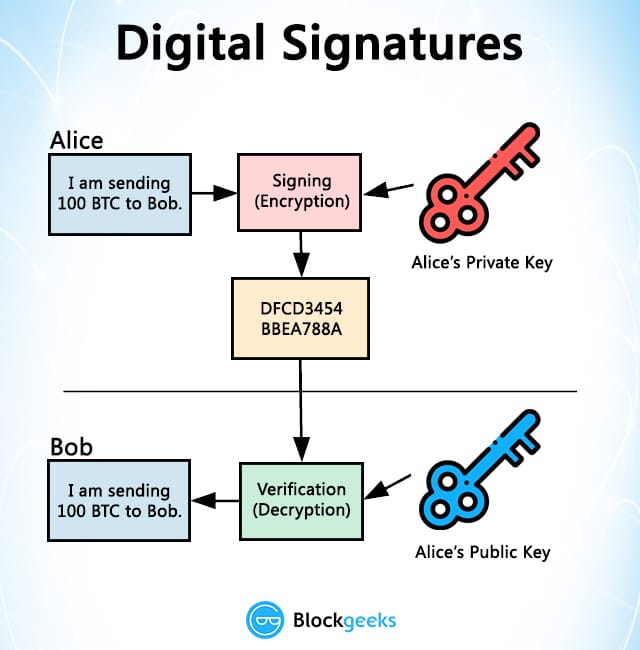
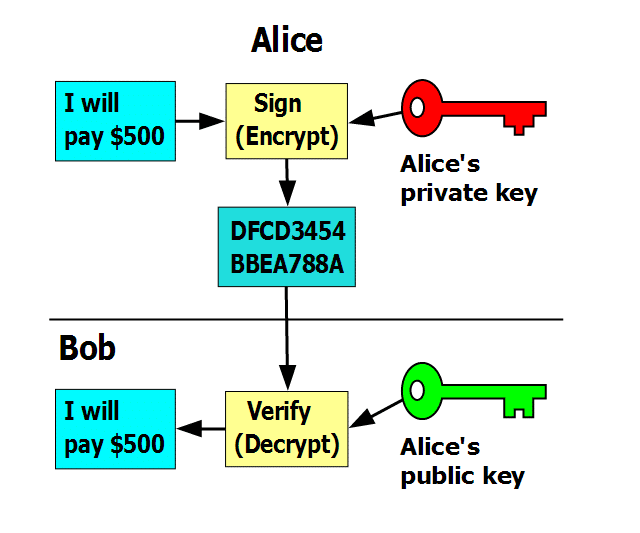
So how does the signing process work (a simple overview)?
Suppose Alice wants to send 500 BTC to Bob. She will follow the following steps:
- She will create transaction and sign it off with her private key.
- She will the send the transaction to Bob’s public address.
- Bob can then decrypt the message by using Alice’s public key to verify that it was indeed Alice who sent him the bitcoins and the transaction is deemed complete.
If this were to be shown in an image this is what it will look like:
Cryptocurrencies Cryptography: Conclusion
So, as can be seen, public key cryptography aka asymmetric cryptography is one of the backbones of cryptocurrency. It is impossible to even imagine how bitcoin and ethereum would have been secure without it. Every time you make a transaction, be thankful to all the mathematicians and cryptographers who have made this wonderful medium possible.










Good explanation! Well done !
Thank you for the article
I think its better if you explain in a plain language
Wow! Not something you want to think about when you are tired. Very informative though
Very informative. There’s a lot of detail but gives reader a full understanding of cryptography.
Very good. I love the provided examples to see how it works. Thank you.
Thank you for sharing useful information. i appreciate your content. I love your Blog!
Thank you for the article, it was a great introduction to the subject. The majority of the content was described well, but I feel like the mathematical descriptions of public/private keys and elliptical curve cryptography can be improved. For example, it is never explained until late in the section on elliptical curve cryptography that the “values” are two-dimensional points. Furthermore, the claim that the reflected points called (V+A) is the sum of the first two points doesn’t seem to be right. Could it possibly be -(V+A), assuming vector addition? Lastly, in “Euler’s theorem”, under modification #2, the claim that “e*d = k*phi(n) + 1” doesn’t explain how the Mod n and Mod N in the two expressions are dealt with.
Very difficult to understand for newbie like me. I hope at the end of course i will learn something
Stupid question cause I’m not a mathematician, even less so a cryptographer, but I have a doubt…
This sentence “Bob now determines the same message K by:
K = M1 ^ a mod n = g^ab mod n.”
Shouldn’t be like this: “Bob now determines the same message K by:
K = M1 ^ b mod n = g^ab mod n.
Cause M1=g^a mod n, so if we do as the original text says we would have K = M1^a mod n = g^a2 mod n.
Please advice….
To keep the same notation, shouldn’t it be written as:
m ^ phi(n) mod n ≡ 1
This makes more sense as well since, 1 mod x = 1
Interesting article, thank you! Great introduction.
is there an instance where the public key is used for the encryption and the private for decryption? (As given in the example of the RSA algorhythm section)
Hey Valentina. The Public key is always used for encryption and the private key is always used for decryption. The reason is simple, you don’t want a key that is publicly and openly available to everyone to be responsible for decrypting ciphertexts.
That’s just for verification to make sure that it is indeed Alice who is sending the money. The only way that you know that it is indeed Alice who is saying something is by decrypting her message with her public key. The only way that is possible is if Alice used her private key to encrypt her message. Remember, private and public keys are both mathematically complementary…in layman’s term “they cancel each other out”.
Perfect Shot ! ! ! ! ! Thank you.
How do AI’s and or quantum computers fit into decrypting The blockchain? Theft?
Shor’s algorithm can break the cryptography behind RSA or EES but
a) we do not have such powerful quantum computers yet and it looks impossible we get them in the next 20-30 years (or more), and
b) one can use quantum cryptography to generate similar complexity for quantum computers, see research paper Quantum Bitcoin: An Anonymous and Distributed Currency Secured by the No-Cloning Theorem of Quantum Mechanics by Jonathan Jogenfors – but again not needed because of (a) above
there are some P2P machine learning initiatives as well, like:
http://neureal.net/